GTS

抽象化とは

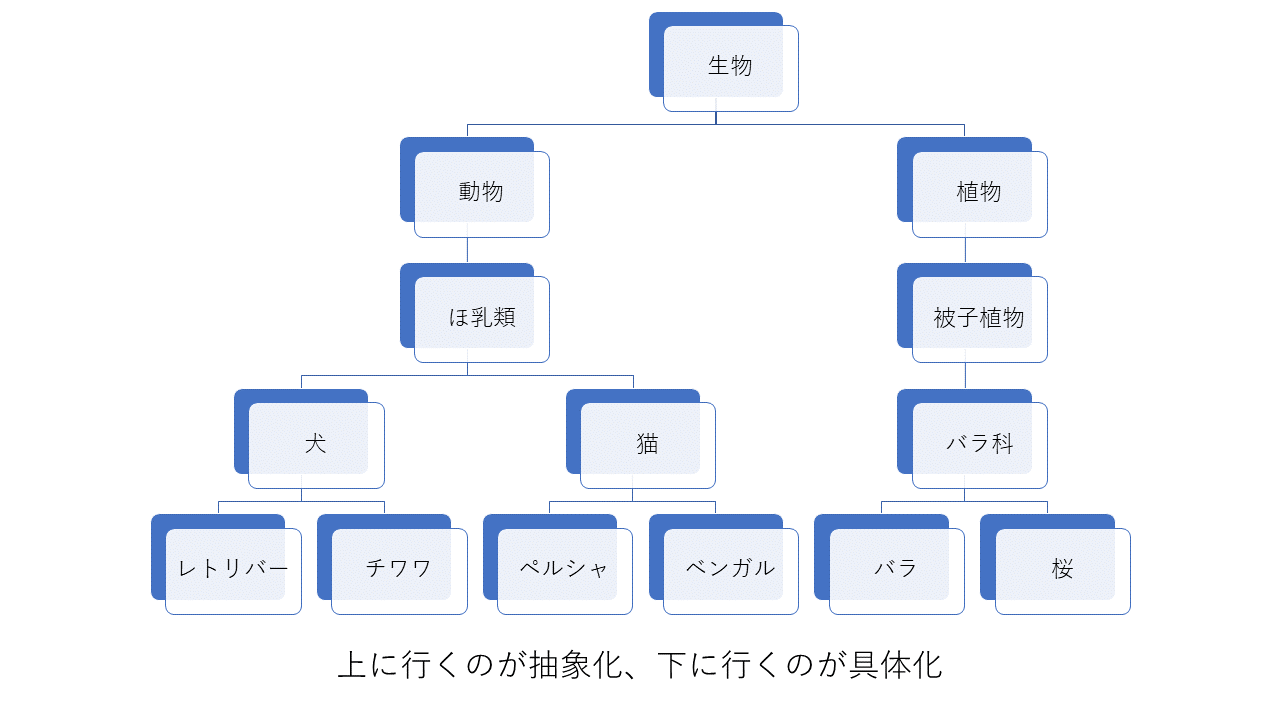
抽象化という言葉は非常に難しく感じるかもしれないが、簡単に言えば
チワワ　→　犬　→　ほ乳類　→　動物　→　生物
と枠組み（カテゴリ）を大きくしていくことである。

数学における抽象化

数学においては、具体的な数字（\(1, 2 ,3, -1, -2, …\)）を文字（\(a, b, c, x, y, z\) など）に抽象化する。
文字には何か数字が入っている、と思えば良いので、文字になっていて分かりづらいときは、数字を入れてみると良い。

「定数と変数」による分け方は、ルネ・デカルト（Renes Descartes,1596-1650）によるものを現代でも使っている。

定数と変数

定数とは「定まった数のこと。一度定まったら変わらない。」
変数とは「変わることがあり得る数のこと。」

定数とは

定数とは「定まった数のこと。一度定まったら変わらない。」
文字になっていても、この数は数字が定まったら変化しない。
\(a, b, c\) などアルファベット順に使うことが多い。
また、\(\pi\) なども定数である。

変数とは

変数とは「変わることがあり得る数のこと。」
色々な数になることができる。
\(x, y, z\) などアルファベットの逆順から使うことが多い。

参考：意外と難しい！？変数(未知数)と定数の違い

ルネ・デカルト（Renes Descartes,1596-1650）

かけ算の記号 \(\times\) は省く。

1. 文字の混じった乗法では かけ算の記号 \(\times\) は省く。
2. 文字と数字の積は数字を先に書く。
3. \(1\) や \(-1\) と文字との積では \(1\) を省略する。
4. 文字はふつうアルファベット順に書く。
5. 文字と式、数字と式の積ではふつう式が後。

例：\(a \times b = ab,\ x \times 12 = 12x,\ 1 \times c = c,\ a \times (-1) = -a,\)
\( a \times b \times c = abc,\ x \times a \times (-3) = -3ax,\ (x+y) \times a = a(x+y)\)

同じ文字のかけ算は指数を使って表す。

1. 同じ文字の積（かけ算）は累乗の指数を用いて表す。
2. 同じ文字式の場合も同じ、かっこの右上にかく。

例：\(x \times x \times x \times x \times x \times x= x^6,\ n \times (-3) \times n = -3n^2\)
\( a \times a \times a \times c \times b \times b = a^3b^2c,\ (a + b)\times(a + b) = (a + b)^2 \)

割り算は分数の形で表す。

1. 文字の混じった除法では割り算の記号 \(\div\) を使わず分数の形で表す。
2. 分子に割られる数、分母に割る数がくる。
3. 分子や分母全体につくかっこは省く。
4. 負の符号 \(-\) は分数の前に書く。

例：\(a \div b = \dfrac{a}{b},\ x \div 5 =\dfrac{x}{5},\ (x+y) \div n =\dfrac{x+y}{n},\)
\( -4 \div a = -\dfrac{4}{a},\ 2 \div (-c) = -\dfrac2c,\ (a+3)\div(-2) = -\dfrac{a+3}{2} \)

まとめ

1. 割り算はかけ算になおしてから \(\times\) を省く。
2. 文字と数字のかけ算は数字を先に書く。
3. 文字はアルファベット順、\(\pi\) は数字と文字の間に書く。
4. 足し算、引き算の記号 \(+, -\) は省略できない。

例：\( 4 \div 3 \times r \times r \times r \times \pi = 4 \times \dfrac13 \times \pi r^3 = \dfrac43 \pi r^3 ,\)
\( x \times x \times a \times 2 + x \times (-1) - 3\div c = 2ax^2 -x - \dfrac3c \)